Die Anfänge meiner Geometrie.
Ich will an dieser Stelle nicht ins Detail gehen,
sondern nur ein paar meiner Entdeckungen vorstellen.
... Und zwar so, dass sie jeder versteht.
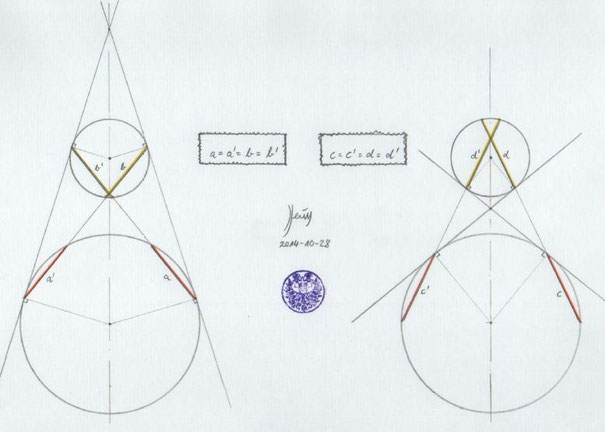
1.) Die Beziehungen gemeinsamer Tangenten zweier Kreise
Lehrsatz: Verbindet man die Berührungspunkte
der inneren oder äußeren Tangenten an zwei Kreise überkreuz miteinander,
dann sind die so entstandenen vier Sehnen gleich lang.
Alles klar, oder?
Veröffentlicht wurde dies in
"Die Wurzel - Zeitschrift für Mathematik", Heft 12/2005, S. 267.
Dann eine Vermutung meinerseits:
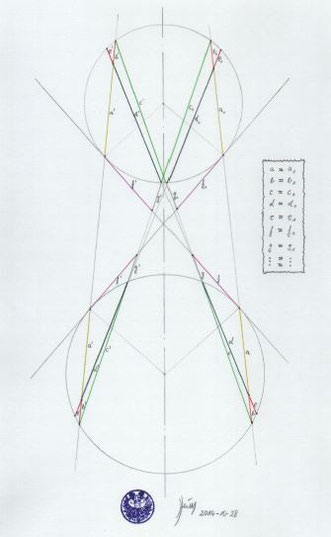
Man kann dieses Spielchen fortsetzen, denn durch die Verbindung
überkreuz entstehen immer zwei neue Schnittpunkte mit den Kreisen.
Verbindet man diese wieder überkreuz miteinander, entstehen
wieder gleich lange Sehnen, usw. Macht man das öfter, dann
überschneiden sich die Sehnen, und die Teilstrecken der Sehnen
sind auch wieder gleich lang.
Also: Strecken mit gleicher Farbe sind in der Zeichnung gleich lang.
(Dies wurde ebenfalls im oben genannten Artikel veröffentlicht.)
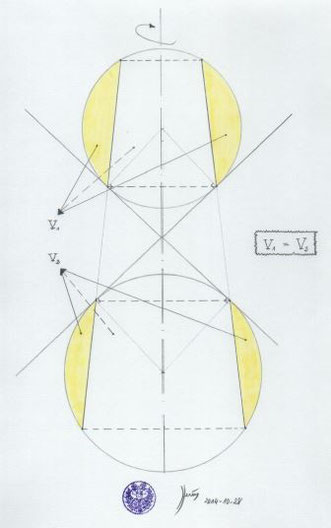
Das Ganze kann man jetzt rotieren lassen.
Dabei werden Formen wie "Apfelschalen" von den beiden Kugeln abgeschnitten.
Die Volumen der beiden Apfelschalen sind gleich groß.
Diese Entdeckung wurde damals im eingesandten Artikel gekürzt,
und somit leider nicht veröffentlicht.
Und auch hierzu habe ich die Vermutung, dass das Spiel fortgesetzt werden kann.
Lässt man die Teilstrecken der Sehnen rotieren, dann erhält man
Teilstücke der Apfelschalen, die das gleiche Volumen haben sollten.
(Alle diese Beziehungen zu den Tangenten entdeckte ich im Jahr 2003.)
2.) Die Begradigung eines Möndchens
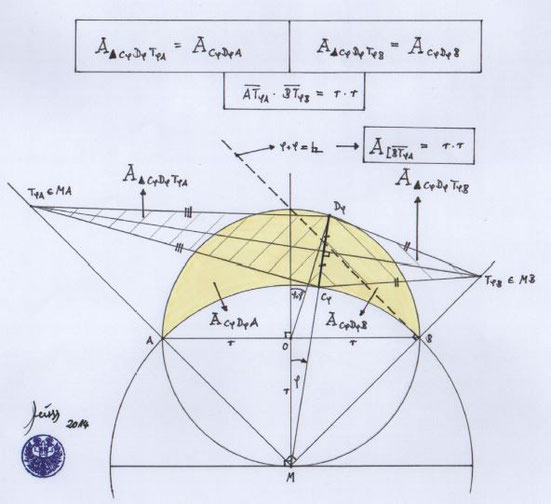
Zu sehen ist eine gelbe Form, ein sog. "Möndchen des Hippokrates".
Dieses wurde durch einen Schnitt in zwei Hörnchen zerteilt.
Und meine Entdeckung dabei:
Die Hörnchen haben dieselbe Fläche wie die beiden schraffierten Dreicke.
Wen's interessiert: Veröffentlicht wurde das Ganze in
"Die Wurzel - Zeitschrift für Mathematik", Heft 11/2015.
Und im Internet seit Mai 2017 unter:
"www.gogeometry.com/problem/p1335" als Problem 1335
(Entdeckt hab' ich das aber schon 2013.)
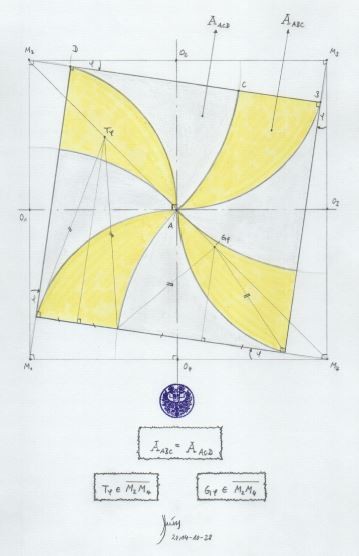
Eine weitere Entdeckung zu den Möndchen des Hippokrates:
Die Fläche des gelben Windrades ist gleich
der weißen Restfläche des schiefen Quadrats.
Veröffentlichung als Aufgabe in
"Die Wurzel - Zeitschrift für Mathematik", Heft 5/2017, S.119
(Entdeckte ich im Jahr 2013.)
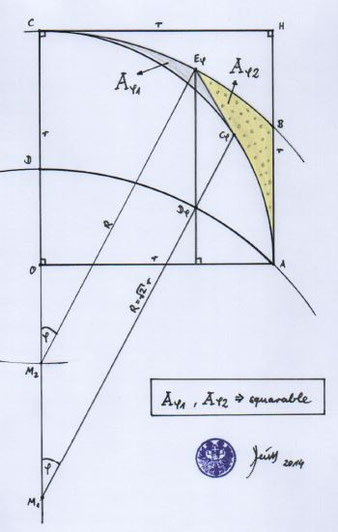
Noch eine ergänzende Entdeckung von 2014 zu den Möndchen:
Die beiden in der Zeichnung markierten Flächen sind quadrierbar.
Hierzu eine kurze Geschichte
Es ging bei den Möndchen des Hippokrates ursprünglich
um die später sprichtwörtlich gewordene "Quadratur des Kreises".
Bei der Quadratur des Kreises handelt es sich um eines der
drei großen Probleme der griechischen Antike.
Dabei sollte ein Kreis allein mit Zirkel und Lineal (ohne Maßeinteilung)
in ein Quadrat mit der gleichen Fläche wie der Kreis konstruktiv
umgewandelt werden. Da Hippokrates von Chios ca. 450 v. Chr.
die Quadrierbarkeit seiner Möndchen zeigen konnte,
glaubte man noch lange, die Quadratur des Kreises sei möglich.
Erst im Jahre 1882 zeigte Ferdinand von Lindemann,
dass dies unmöglich ist.
Allerdings versteht es sich fast wie von selbst,
dass ich - als "der Herr der Kreise" -
mich mit diesem Problem beschäftigen musste!
3.) Im Jahr 2013 entdeckte ich das, was ich als
"Drei-Figuren-Satz der Elementargeometrie" bezeichne.
Der Satz besagt Folgendes:
Dazu ein kleines Beispiel:
Verwandelt man einen Kreis in ein Quadrat mit gleicher Fläche,
und in ein Quadrat mit gleichem Umfang, dann ist der Inkreis-Radius
des flächengleichen Quadrats das geometrische Mittel aus
den Inkreis-Radien des Kreises und des umfangsgleichen Quadrats.
Oder einfach ausgedrückt:
Wäre das Abrollen der Umfangslinie eines Kreises möglich,
dann wäre auch die Quadratur des Kreises möglich.
4.) Gleich zu Beginn meiner geometrischen Forschung versuchte ich
"Ordnung in das Chaos" zu bringen. Ich wollte eine Ordnung schaffen,
die ich selbst besser verstehe.
Und so entwickelte ich im Jahr 1998 das nachfolgende Schaubild:
Längen und Radien habe ich hierfür standartisiert.
Also: a = b = c = r = x
Schaut man sich die Tafel nur lange genug an,
dann begreift man früher oder später
die dahinter-steckende Systematik.
Natürlich interessierte ich mich auch für andere geometrische Beziehungen,
aber zu den hier beschriebenen machte ich meine Entdeckungen.
... Und ein wenig Stolz ist meinerseits auch dabei,
denn die dahinter steckende Mathematik ist so primitiv,
dass diese Entdeckungen im Prinzip jeder Hobby-Geometer
der letzten Jahrhunderte hätte machen können.
Hat aber keiner!
Im Laufe der Jahre entdeckte ich noch viele weitere geometrische Beziehungen.
Eine Auflistung dieser findet man hier.